Event Details
Paola Bacigaluppi Institute of Mathematics, University
Leggi tutto
Event Details
Paola Bacigaluppi
Institute of Mathematics, University of Zurich, Switzerland
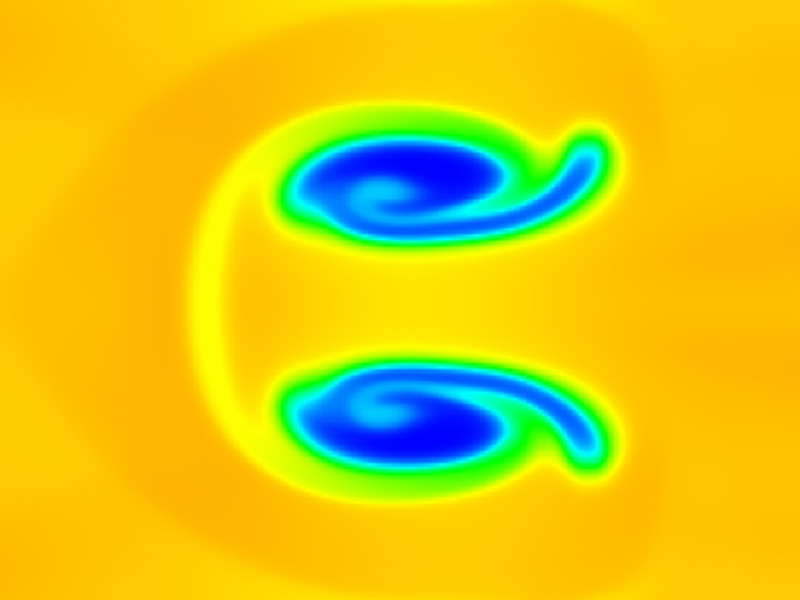
Within the framework of the equilibrium two-phase mixtures with phase transition, this work focuses on a four-equation model, which allows to study certain typologies of cavitation problems, where the assumption of a homogeneous temperature, pressure and velocity are allowed. In particular, we tackle the study of time dependent problems with strong discontinuities and phase transition. Driven by the interest of engineering-based applications towards the treatment of non-conserved variables, this work presents a novel approach to solve systems of equations with a non-conservative formulation which guarantees the actual conservation of the mass, momentum and energy quantities, following [3] . This non-conservative formulation allows avoiding the classical oscillations obtained by many approaches, that might appear for the pressure profile across contact discontinuities. Further, the proposed method is formulated with an “a posteriori limiter” following the recent work [1] and is based on a finite volume- type residual distribution (RD) scheme designed for an explicit second-order time stepping (see [2]). This novel approach is cross-validated on several one- and two-dimensional benchmark problems with the approximated solution obtained via a conservative approach, based on an HLLC solver implemented for the CLAWPACK (CP) software.
Date e orari
mercoledì 12 Giugno 2019
Dalle 12:00
Luogo
Politecnico di Milano - Sala Consiglio, DAER, 2nd Floor, Building B12
Via La Masa, 34 - 20156 Milano
Organizzatore
Politecnico di Milano